Grupa Coxetera
Grupą Coxetera – grupa z wyróżnionym układem generatorów którego elementy spełniają następujący układ relacji:
gdzie:
- czyli dla dowolnego
- dla przy czym dla nie istnieje relacja między a [1].
Nazwa pojęcia pochodzi od nazwiska Harolda Coxetera[2]. Grupy tego rodzaju są rozważane w teorii grup dyskretnych jako uogólnienie grup odbić[3] generowanych przez odbicia względem hiperpowierzchni w przestrzeni euklidesowej. Każda grupa odbić jest grupą Coxetera, jeśli jej generatorami są odbicia względem hiperpowierzchni ograniczających wielościan fundamentalny.
Macierz gdzie nazywa się macierzą Coxetera danej grupy Coxetera. Macierz ta i sama grupa może być zadana za pomocą grafu Coxetera – grafu o wierzchołkach w którym wierzchołki i są połączone -krotną krawędzią, jeśli (w szczególności nie są w ogóle połączone, jeśli ) i są połączone grubą krawędzią, jeśli Czasem zamiast łączyć wierzchołki grafu krawędziami wielokrotnymi, łączy się je jedną krawędzią ze znakiem nad nią.
Własności
- Jeśli to mnożenie przez jest przemienne.
- jest rzędem elementu
Przykłady
- Każda grupa generowana przez dwa elementy rzędu 2 jest grupą Coxetera o macierzy postaci Jej graf Coxetera:
- Grupa symetryczna jest grupą Coxetera względem generatorów dla ( jest transpozycją elementów i ). Jej graf Coxetera:
- Macierzą Coxetera grupy jest:
- Grupa jest grupą Coxetera względem generatorów:
- Jej graf Coxetera:

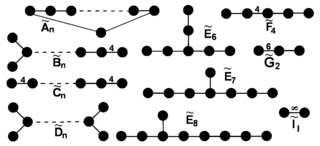
Skończone grupy Coxetera
H.S.M. Coxeter w roku 1934 znalazł wszystkie grupy odbić w n-wymiarowej przestrzeni euklidesowej i wykazał, że są one grupami Coxetera[4]. W następnej pracy[5] wykazał, że każda skończona grupa Coxetera jest izomorficzna z pewną grupą odbić w której elementy mają wspólny punkt stały. W ten sposób otrzymał klasyfikację grup skończonych Coxetera.

Nieskończone grupy Coxetera
Wśród nieskończonych grup Coxetera można wyróżnić grupy paraboliczne, izomorficzne z pewną grupą odbić w przestrzeni euklidesowej i grupy hiperboliczne, izomorficzne z pewną grupą odbić przestrzeni hiperbolicznej elementy których nie mają wspólnej hiperpłaszczyzny niezmienniczej o wymiarze mniejszym od n (w przypadku hiperbolicznym za hiperpłaszczyznę należy uważać również punkt w nieskończoności[7]).
Wszystkie paraboliczne grupy Coxetera zostały znalezione przez H.S.M. Coxetera, który udowodnił, że są to afiniczne grupy Weyla z teorii półprostych grup Liego.
Związek z wielościanami
Jeśli przestrzeń jest n-wymiarową sferą, przestrzenią euklidesową lub przestrzenią hiperboliczną, to grupa odbić jest generowana przez odbicia względem hiperpowierzchni ograniczających wielościan fundamentalny tej grupy. Względem tego układu generatorów grupa odbić jest grupą Coxetera o relacjach zdefiniowanych następująco:
- jeśli ściany i przylegają do siebie i kąt między nimi jest równy to gdzie
- jeśli ściany i nie przylegają do siebie, to
Wielościany fundamentalne grup Coxetera nazywają się wielościanami Coxetera. Wielościanami Coxetera można wypełnić przestrzeń. Mają więc związek z parkietażami i krystalografią.
Przykłady
- Wielościany Coxetera w n-wymiarowej przestrzeni euklidesowej:
- 2n-komórka foremna
- (n + 1)-komórka (n-sympleks)
- Wielościany Coxetera w n-wymiarowej sferze:
- n-wymiarowy sympleks foremny o boku
- Wielościany Coxetera w n-wymiarowej przestrzeni hiperbolicznej:
- k-wielokąt foremny o kącie w przestrzeni 2-wymiarowej,
- dwunastościan foremny (dodekaedr) prostokątny w przestrzeni 3-wymiarowej,
- 120-ścian foremny prostokątny w przestrzeni 4-wymiarowej.
Przypisy
- ↑ Математическая энциклопедия. И.М. Виноградов (red.). T. 2. Москва: Советская энциклопедия, 1979, s. 944.
- ↑ Coxetera grupa, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2021-10-02] .
- ↑ Harold Scott MacDonald Coxeter. Discrete groups generated by reflections. „Ann. of Math.”. 35, s. 588–621, 1934.
- ↑ Coxeter, Discrete groups generated by reflections, op. cit.
- ↑ Harold Scott MacDonald Coxeter. The groups determinated by the relations of the form . „J. London Math. Soc.”. 10, s. 21–25, 1935.
- ↑ Nicolas Bourbaki: Groupes et algebres de Lie. T. XXXIV (rozdz. IV-VI). Paris: Hermann, 1968. (tłum. ros. 1972), s. 241.
- ↑ Математическая энциклопедия, op. cit., s. 945.
Bibliografia
- Математическая энциклопедия. И.М. Виноградов (red.). T. 2. Москва: Советская энциклопедия, 1979.
- Harold Scott MacDonald Coxeter. Discrete groups generated by reflections. „Ann. of Math.”. 35, s. 588–621, 1934.
- Harold Scott MacDonald Coxeter. The groups determinated by the relations of the form . „J. London Math. Soc.”. 10, s. 21–25, 1935.
- Harold Scott MacDonald Coxeter, William Moser: Generators and relationsfor discrete groups. Berlin Heidelberg New York: Springer Verlag, 1972.
- Nicolas Bourbaki: Groupes et algebres de Lie. T. XXXIV (rozdz. IV-VI). Paris: Hermann, 1968.

























![{\displaystyle \left[{\begin{smallmatrix}2&m\\m&2\end{smallmatrix}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f369132ed1688ec9777b776df77bb6c1a8a08fa4)




































