Orthogonaal

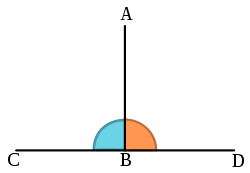
In de twee- of driedimensionale euclidische meetkunde zegt men van twee objecten dat zij orthogonaal (van Oudgrieks: ὀρθός (orthos), recht en γωνία (gonia), hoek) zijn, als zij ten opzichte van elkaar een rechte hoek vormen, of anders gezegd loodrecht (haaks) op elkaar staan. Dit wordt wel aangegeven door het teken ${\displaystyle \perp }$ tussen de objecten te plaatsen. Ook van meer dan twee objecten zegt men dat zij orthogonaal zijn, als elk tweetal van deze objecten orthogonaal is.

In andere takken van de wiskunde spreekt men ook over orthogonale objecten zonder dat er nog enig verband bestaat met het gewone begrip rechte hoek of loodrechte stand. Orthogonaliteit van objecten heeft dan een specifieke betekenis die veelal verbonden is met de aard van die objecten. Hierna volgen een paar voorbeelden.

In de statistiek wordt met de term ook wel volledige afwezigheid van correlatie tussen twee variabelen bedoeld.

Inproduct

Voor objecten waarvoor een inproduct gedefinieerd is, wordt de hoek tussen deze objecten afgeleid van dit inproduct. Twee objecten met een inproduct gelijk aan 0 heten dan orthogonaal.

Vectoren

In de Euclidische meetkunde in ${\displaystyle n}$ dimensies wordt het inproduct van twee vectoren ${\displaystyle x}$ en ${\displaystyle y}$ gedefinieerd door:

${\displaystyle \langle x,y\rangle =x_{1}y_{1}+x_{2}y_{2}+\ldots +x_{n}y_{n}}$

Voor twee orthogonale vectoren ${\displaystyle x}$ en ${\displaystyle y}$ geldt dus:

${\displaystyle \langle x,y\rangle =x_{1}y_{1}+x_{2}y_{2}+\ldots +x_{n}y_{n}=0}$

Zij staan dan in de gebruikelijke voorstelling loodrecht op elkaar. Zo zijn bijvoorbeeld in het platte vlak de vectoren (1,1) en (2,–2) orthogonaal. Evenzo de vectoren (1,3) en (6,–2). In de driedimensionale ruimte zijn bijvoorbeeld de vectoren (–1,1,1) en (2,1,1) orthogonaal.

Als het stel vectoren ${\displaystyle (e_{1},e_{2},\ldots )}$ orthogonaal is en tevens elk van de vectoren de norm 1 heeft, noemen we ze ook wel orthonormaal. Er geldt dan voor iedere ${\displaystyle i}$ en ${\displaystyle j}$:

${\displaystyle \langle e_{i},e_{j}\rangle =\delta _{ij}={\begin{cases}0&{\mbox{als }}i\neq j\\1&{\mbox{als }}i=j\end{cases}}}$

Een verwant begrip is het orthogonaal complement van een lineaire deelruimte.

Functies

Voor functies op een domein ${\displaystyle D}$ kan het volgende inproduct gedefinieerd worden:

${\displaystyle \langle f,g\rangle =\int _{D}f(x)g(x)\,\mathrm {d} x}$.

Twee functies ${\displaystyle f}$ en ${\displaystyle g}$ zijn dan orthogonaal als:

${\displaystyle \int _{D}f(x)g(x)\,\mathrm {d} x=0}$

Voor ${\displaystyle D=[0,2\pi ]}$ is bijvoorbeeld:

${\displaystyle \int _{0}^{2\pi }\sin(x)\cos(x)\,\mathrm {d} x=0}$,

dus zijn sin en cos orthogonaal.

Zie ook

• Orthogonale matrix
• Orthogonale groep
• Orthonormaal
• Norm
• Laguerre-polynoom
• Gram-Schmidtmethode