Geometrografie

Onder geometrografie wordt in de wiskunde verstaan de studie van de complexiteit van constructies van meetkundige figuren met passer en (ongemerkte) liniaal (verder afgekort als p&l). Een constructie van een figuur gebaseerd op deze theorie is een geometrografische constructie.^[1]

De basis voor de geometrografie is in 1888 gelegd door de Franse civiel ingenieur en wiskundige Émile Lemoine (1890-1912). Hij noemde zijn theorie géométrographie.^[2] Eerder hebben wiskundigen als Lorenzo Mascheroni (1750-1800) en Jakob Steiner (1796-1863) zich met de theorie van de p&l-constructies bezig gehouden.^[3][4]

Het is bekend dat een p&l-constructie van een figuur vaak op meer manieren (in een verschillend aantal stappen, met andere ‘tussenobjecten’) kan worden uitgevoerd.

De opdracht luidt: Construeer met p&l de loodlijn ${\displaystyle n}$ op een gegeven lijn ${\displaystyle l}$ in een gegeven punt ${\displaystyle A}$ van die lijn ${\displaystyle l}$. Hieronder staan de constructiestappen, in twee verschillende gevallen (zie figuur ${\displaystyle {\rm {I}}}$ en figuur ${\displaystyle {\rm {II}}}$):

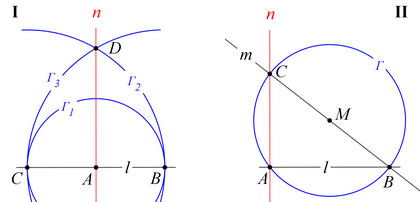
Constructiestap	${\displaystyle {\rm {I}}\,}$ (links)	${\displaystyle {\rm {II}}\,}$ (rechts)
1.	Punt ${\displaystyle B}$ op ${\displaystyle l}$	Punt ${\displaystyle M}$ buiten ${\displaystyle l}$
2.	Cirkel${\displaystyle (A,AB)={\Gamma _{1}}}$	Cirkel${\displaystyle (M,MA)={\Gamma }}$
3.	Snijpunt(en)${\displaystyle (l,{\Gamma _{1}})=C}$	Snijpunt(en)${\displaystyle (l,{\Gamma })=B}$
4.	Cirkel${\displaystyle (C,CB)={\Gamma _{2}}}$	Lijn${\displaystyle (B,M)=m}$
5.	Cirkel${\displaystyle (B,BC)={\Gamma _{3}}}$	Snijpunt(en)${\displaystyle (m,\Gamma )=C}$
6.	Snijpunt(en)${\displaystyle (\Gamma _{2},\Gamma _{3})=D}$	Lijn${\displaystyle (C,A)=n}$
7.	Lijn${\displaystyle (D,A)=n}$

Op de vraag welke van deze beide p&l-constructies, objectief gezien, de grootste complexiteit heeft, geeft de door Lemoine ontwikkelde methode in ieder geval een antwoord.

Overigens, de geometrografische methode is slechts korte tijd en in een klein aantal landen (Frankrijk, Engeland, België, Duitsland) gebruikt.^[5] De theorie staat evenwel weer in de belangstelling vanwege het onderzoek naar de complexiteit bij computergestuurd construeren.^[6]

In de geometrografie beperkt men zich bij de geometrografische beschrijving tot vijf elementaire constructies, waarmee, zo nodig herhaald, alle p&l-constructies kunnen worden beschreven.

	Bewerking	Notatie
1.	Het leggen van de liniaal door één bestaand punt	${\displaystyle R_{1}}$
2.	Daadwerkelijk tekenen van een rechte lijn door twee bestaande punten	${\displaystyle R_{2}}$
3.	Een passerpunt plaatsen op een bestaand punt	${\displaystyle C_{1}}$
4.	Een passerpunt plaatsen op een willekeurig punt van een rechte lijn of van een cirkel	${\displaystyle C_{2}}$
5.	Daadwerkelijk tekenen van een cirkel	${\displaystyle C_{3}}$

Indien de bewerking ${\displaystyle X\;(={R_{i}},{C_{i}})}$ in een constructiebeschrijving ${\displaystyle n}$ keer voorkomt, dan wordt dat genoteerd als ${\displaystyle nX}$. Daarbij is: ${\displaystyle R}$ = (fr) règle = liniaal en ${\displaystyle C}$ = (fr) cercle = cirkel.

• Het leggen van de liniaal door twee gegeven punten wordt geschreven als ${\displaystyle 2R_{1}}$. Als daarna, zonder de liniaal te verplaatsen, de rechte lijn door die twee punten getekend wordt, dan wordt dat geschreven als ${\displaystyle 2R_{1}+R_{2}}$.
• Het tekenen van een driehoek als de hoekpunten gegeven zijn, geeft ${\displaystyle 4R_{1}+3R_{2}}$.
• Het plaatsen van een passerpunt in een bepaald punt om vervolgens de andere passerpunt in een ander bepaald punt te plaatsen is ${\displaystyle 2C_{1}}$ (“een afstand in de passer nemen”). Een constructie beginnen met het tekenen van een willekeurige cirkel wordt beschreven met ${\displaystyle C_{3}}$.

Elke meetkundige constructie leidt dan tot een uitdrukking van de vorm:

${\displaystyle G=p_{1}R_{1}+p_{2}R_{2}+q_{1}C_{1}+q_{2}C_{2}+q_{3}C_{3}}$

waarin de coëfficiënten ${\displaystyle p_{i}}$, ${\displaystyle q_{i}}$ het aantal keer aangeven dat de bijbehorende bewerking is uitgevoerd.

Lemoine noemde het getal ${\displaystyle B=p_{1}+p_{2}+q_{1}+q_{2}+q_{3}}$ – dat is dus het aantal bewerkingen ${\displaystyle (B)}$ – de coefficient de simplicité (kortweg simplicité), maar dat lijkt tegenstrijdig, omdat de ‘eenvoud’ van de constructie groter is naarmate het getal ${\displaystyle B}$ kleiner is.

De nauwkeurigheid (exactheid, ${\displaystyle E}$) van de constructie is slechts afhankelijk van de bewerkingen ${\displaystyle R_{1}}$, ${\displaystyle C_{1}}$ en ${\displaystyle C_{2}}$. Dit zijn immers de bewerkingen waarbij, met het in de praktijk uitvoeren van de constructie, fouten kunnen worden gemaakt. Lemoine noemde het getal ${\displaystyle E=p_{1}+q_{1}+q_{2}}$ coefficient d’exactitude (kortweg exactitude) van de constructie.

Lemoine behandelde in zijn boek Géométrographie meer dan 60 constructies uit de elementaire meetkunde, zoals (en let wel, de volgorde van de constructiestappen is uit ${\displaystyle G}$ niet af te leiden):

• De constructie van een rechte hoek (waarvan niets gegeven is), met:

${\displaystyle G=4R_{1}+3R_{2}+C_{3};B=8;E=4}$

• De constructie van het middelpunt van een gegeven cirkel, als het middelpunt niet zichtbaar is, met:

${\displaystyle G=4R_{1}+2R_{2}+3C_{2}+3C_{3};B=12;E=7}$

• De constructie van het lijnstuk met lengte ${\displaystyle x}$, dat middelevenredig is tussen twee gegeven lijnstukken met lengte ${\displaystyle a}$ en ${\displaystyle b}$ (dus zo dat ${\displaystyle {x^{2}}=ab}$), met:

${\displaystyle G=4R_{1}+3R_{2}+12C_{1}+C_{2}+8C_{3};B=28;E=17}$

• Constructie met passer en liniaal
• Stelling van Mohr-Mascheroni
• (en) Compass equivalence theorem
• (en) Poncelet–Steiner theorem

• M. Eilander (1951): Geometrografie; of: welke constructie is de eenvoudigste? In: Euclides, jg. 27 (1951-1952), nr. 1/2, pp. 62–69; PDF-bestand.
• Howard Eves (1972): A Survey of Geometry. Boston: Allyn and Bacon; pp. 154–193.
• A. Grüttner (1912): Die Grundlagen der Geometrographie. Breslau: R. Nischkowski. Via: Heinrich Heine Universität, Düsseldorf.
• George E. Martin (1997): Geometric Constructions. New York: Springer Verlag.