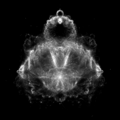
ブッダブロ

ブッダブロ（英: buddhabrot）とはマンデルブロ集合に関する図形。ガウス平面から点${\displaystyle c}$をランダムに選び、その${\displaystyle c}$について数列${\displaystyle z_{n+1}={z_{n}}^{2}+c}$を計算し、${\displaystyle |z_{n+1}|>2}$となった場合に${\displaystyle z_{1}}$から${\displaystyle z_{n}}$までの位置に点を描くという作業を、指定した回数だけ反復（iteration）して行ったもの。形がブッダに似ていることから名付けられた。色毎に計算回数を変えてカラー化することもある。

発見

マンデルブロ集合が初めて描かれたのは1978年のことであり^[1]、その名はこの集合の研究に深く取り組んだアメリカの数学者ブノワ・マンデルブロにちなんで付けられた^[2]:p.146。

1988年、ライナス・ヴェスタス（Linas Vepstas）がマンデルブロ集合を変形して得られるより芸術性の高い図形を発見し、サイエンスライタークリフ・ピックオーバー（英語版）に送っており、これがきっかけで、ピックオーバー軸（英語版）と呼ばれる図形が発見された。ピックオーバーの著書Computers, Pattern, Chaos, and Beauty^[3]に収録されている。

ブッダブロを計算する手法を始めて提案したのはメリンダ・グリーン（Melinda Green）であり^[4]、1993年のネットニュース、sci.fractalsに投稿された^[5]。グリーンにはインド出身の同僚がおり、そのアドバイスをヒントにこの図形を初めガネーシャと名付けた^[5]。ガネーシャは首から上が象の形をしたインドの神である。この図形にブッダブロの名をつけたのは、Robarts Research Instituteの^[4]ロリ・ガルディ（Lori Gardi）である^[6]。

• 
  ブッダブロ
• 
  ガネーシャ
• 
  ブッダ

計算方法

一般のマンデルブロ集合は、複素力学系で

${\displaystyle z_{n+1}={z_{n}}^{2}+c}$

を計算したときに（初期値${\displaystyle z_{0}=0}$）、${\displaystyle \{{z_{n}}\}}$が発散しないような${\displaystyle c}$の集合である。つまり

${\displaystyle M=\{\gamma \vert z_{n+1}={z_{n}}^{2}+c,z_{0}=0,\lim _{n\to \infty }\left|z_{n}\right\vert <\infty \}}$

を満たす集合である^[7]:p.230。

ブッダブロでも、基本の計算にはマンデルブロ数列を用いる。まずガウス平面の内の実数部、虚数部それぞれ-2～2の範囲を描画面に見立て、描画点の細かさを決めておく。次に描画面から点${\displaystyle c}$をランダムに選び、${\displaystyle z_{n}}$を${\displaystyle n=1}$から順に計算し、${\displaystyle |z_{n+1}|>2}$になった時点で（発散が明らかになった時点で）、描画面の${\displaystyle z_{1}}$から${\displaystyle z_{n}}$の位置に点を描く。すでに点が描いてあった場合には、より明るくする。（ただし${\displaystyle n}$の上限${\displaystyle N}$を決めておき、それ以上になったら収束したと見なして点は描かない。）次にまた新たな${\displaystyle c}$をランダムに決め、先の計算を反復する^[5]。

反復回数の大きさは、画像の形に大きく影響する。反復回数が大きくなると、反復回数が小さかったときには暗かった部分にも描画が行われるようになる。

最大反復回数20

最大反復回数100

最大反復回数1,000

最大反復回数2万

最大反復回数百万

反復回数を3原色毎にそれぞれ変えて、画像に色をつけることもできる。これは天文学者が星雲（ネブラ）の画像を擬似カラー化する手法に似ている。そのため、このカラー化画像はネブラブロ（Nebulabrot）と呼ばれることもある（ブッダブロに含めることもある）。さらにはガウス平面に直行する軸を用意し、ブッダブロ集合をマンデルブロ集合と重ね合わせて立体的にプロットさせたアンチ・ブッダブロ（Anti-Buddhabrot）と呼ばれる画像もある。

• 
  ネブラブロ
• 
  アンチブッダブロ

マンデルブロ集合${\displaystyle z^{2}+c}$とロジスティック写像${\displaystyle \lambda x(1-x)}$の関係は良く知られている。${\displaystyle z}$と${\displaystyle c}$をそれぞれ実数部と虚数部に分けた場合、

${\displaystyle c_{r}=\lambda (2-\lambda )/4}$

${\displaystyle c_{i}=0}$

${\displaystyle z_{r}=-\lambda (2x-1)/2}$

${\displaystyle z_{i}=0}$

という関係がある。この関係を図示するのには、昔から${\displaystyle c_{r}}$と${\displaystyle \lambda }$を同じx軸上に置き、y軸の大きさを適当に調整して並べ、同じxでの形状を比較するのが常であった。

ブッダブロを発見したメリンダ・グリーンは、アンチ・ブッダブロ集合がロジスティック写像と立体的な関係を持つことに気付いた。元々、どちらの図形もある出発点から反復計算を行って得られるものである。アンチ・ブッダブロの ${\displaystyle z^{2}+c}$ から ${\displaystyle c=(random,0)}$ と ${\displaystyle z_{0}=(0,0)}$ のデータを抽出し、 ${\displaystyle \{c_{r},z_{r}\}}$ 平面に描けばロジスティック写像が得られる。

• 
  同一平面での重ね合わせ
• 
  直交平面での重ね合わせ

脚注

外部リンク

ウィキメディア・コモンズには、ブッダブロに関連するメディアがあります。

• Buddhabrot メリンダ・グリーンのページ
• Buddhabrot ライナス・ヴェスタスのページ

表 話 編 歴 フラクタル
特徴	フラクタル次元 Assouad（英語版） Box-counting（英語版） Correlation（英語版） ハウスドルフ Packing（英語版） 位相 再帰（英語版） 自己相似 自己相似過程 スケール不変性
反復関数系	バーンズリーのシダ カントール集合 ドラゴン曲線 レヴィC曲線 コッホ雪片 メンガーのスポンジ シェルピンスキーのカーペット シェルピンスキーの三角形 空間充填曲線 T-square（英語版）
ストレンジアトラクター	多重フラクタル系（英語版）
L-system	空間充填曲線
Escape-time fractals	バーニングシップ・フラクタル ジュリア集合 充填 リアプノフ・フラクタル マンデルブロ集合 ニュートン・フラクタル（英語版）
確率的フラクタル	ブラウン運動 非整数ブラウン運動 ブラウンの木（英語版） 拡散律速凝集 フラクタル地形 Lévy flight（英語版） パーコレーション理論（英語版） Self-avoiding walk（英語版）
人物	ゲオルク・カントール フェリックス・ハウスドルフ ガストン・ジュリア ヘルゲ・フォン・コッホ ポール・レヴィ アレクサンドル・リャプノフ ブノワ・マンデルブロ ルイス・フライ・リチャードソン ヴァツワフ・シェルピニスキ
その他	"How Long Is the Coast of Britain?（英語版）" 海岸線のパラドックス List of fractals by Hausdorff dimension（英語版） The Beauty of Fractals（英語版） (1986 book)
カテゴリ