ドミノタイリング

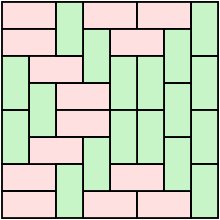
ユークリッド平面上のある領域のドミノタイリング(domino tiling)とは、右の図のようにドミノで領域を埋め尽すことである。同じことであるが、ドミノタイリングは、各々のドミノの中心に頂点として隣合うドミノの 2つの頂点を結ぶことで形成される格子グラフ（英語版）(grid graph)のマッチングのことでもある。モノマー、ダイマー、ポリマーと呼ぶように、2つの原子が繋がったという意味であるユークリッド平面上の（あるいは、トーラス ${\displaystyle \mathbb {R} ^{2}/\mathbb {Z} ^{2}}$ 上の）ダイマーモデル（Dimer model，双体模型）は、多角形分割（英語版）(polygon division)をもたらすモデルであり、完全マッチングであるダイマーモデルは、ドミノタイリングと同義である。

2次元の正方形の格子上のタイリングのクラスに対し、格子のノードへ整数を割り当てる高さ函数を定義することができる。例えば、チェスボード（格子を黒と白の市松模様とする）を描いて、高さ 0 を持つノード ${\displaystyle A_{0}}$ を固定すると、どのノードに対しても ${\displaystyle A_{0}}$ からの経路が存在する。この経路上で、各々のノード ${\displaystyle A_{n+1}}$ (つまり、四方形の頂点）の高さを、${\displaystyle A_{n}}$ から ${\displaystyle A_{n+1}}$ への経路の右側の四方形が黒であれば、前のノード ${\displaystyle A_{n}}$ に 1 をプラスした値とする。そうでなければ、1 をマイナスした値とする。

さらに詳しくは、Kenyon & Okounkov (2005)に記載がある。

ウィリアム・サーストン(William Thurston)は、1990年に平面内の単連結な領域が、単位四方形の組（ドミノ）によりドミノタイリングとして形成されるか否かを決定できることを著した。彼は、3次元の整数格子（英語版）(integer lattice)の中の点 (x,y,z) を頂点として持つような無向グラフを作った。そこでは各々の点が 4つの近傍に連結していて、x+y が偶数であれば、(x,y,z) は (x+1,y,z+1), (x-1,y,z+1), (x,y+1,z-1), (x,y-1,z-1) と連結し、一方、x+y が奇数であれば、(x,y,z) は (x+1,y,z-1), (x-1,y,z-1), (x,y+1,z+1), (x,y-1,z+1) と連結している。この領域の境界は、(x,y) 平面の中の整数の点の列として見なすと、この一意に 3次元グラフ(three-dimensional graph)の中の経路へ（一度、初期の高さを決めると）持ち上げることができる。この領域がタイリング可能であるための必要条件は、この経路が 3次元で単純な閉曲線を形成することを除いて閉じている必要がある。しかし、この条件だけでは充分でない。境界の経路のより注意深く解析して、サーストンは必要かつ充分な領域のタイリングの可能性の判定条件を与えた。

${\displaystyle m\times n}$ の長方形を ${\displaystyle {\frac {mn}{2}}}$ 個のドミノで埋め尽くす方法が何通りあるかの個数の公式は、独立に、Temperley & Fisher (1961) と Kasteleyn (1961) により計算され、

${\displaystyle \prod _{j=1}^{\lceil {\frac {m}{2}}\rceil }\prod _{k=1}^{\lceil {\frac {n}{2}}\rceil }\left(4\cos ^{2}{\frac {\pi j}{m+1}}+4\cos ^{2}{\frac {\pi k}{n+1}}\right)}$

として得られた。

この特別な場合として、${\displaystyle 2\times n}$-長方形のタイリングの方法が何通りあるかという問題がある。この数は、フィボナッチ数列の n-番目の数であるオンライン整数列大辞典の数列 A000045 (Klarner & Pollack 1980)。

他の特別な場合として、m = n = 0, 2, 4, 6, 8, 10, 12, ... であるようなケースがある。

1, 2, 36, 6728, 12988816, 258584046368, 53060477521960000, ... オンライン整数列大辞典の数列 A004003.

これらの何通りあるかという数は、固有値が明確に分かる ${\displaystyle mn\times mn}$ 個の交代行列のパフィアンとして記述することにより、計算することが可能となる。このテクニックは多くの数学的に関連する問題へ適用することが可能である。例えば、統計力学でのダイマー-ダイマー相関函数（英語版）(dimer-dimer correlator function)の古典的 2次元の計算がある。

領域のタイリングの数は境界条件に対して非常に敏感で、一見たいしたことのない形の変化であっても、その数が劇的に変化する場合がある。わかりやすい例に、位数 n のアステカダイアモンド（英語版）(Aztec diamond) があり、このタイリングの数は、2^(n + 1)n/2 である。一方、位数が同じ n でも、中央の長い列が2列ではなく3列に 拡張されたアステカダイアモンド になると、タイリングの数はn のテトレーションから大きく減少し、指数的な数であるデラノイ数（英語版）(Delannoy number) D(n,n) に等しくなる。また、中央列が1列である 縮小されたアステカダイアモンドは、たったひとつのタイリングしか持たない。

• 
  位数 4 のアステカダイアモンド、1024 種類のドミノタイリングを持つ
• 
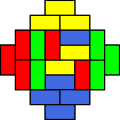  位数 4 のアステカダイアモンドにおけるドミノタイリングの一例

• 統計力学
• ガウス自由場（英語版）(Gaussian free field)、一般的な状況下で、高さ函数のスケール極限（つまり、大きなアステカダイアモンドの内接円板の内部）
• 多重チェスボート問題（英語版）(Mutilated chessboard problem)、チェスボートの 62個の正方形のドミノタイリングに関するパズル
• 畳、日本式の部屋の床のタイリングに使われるドミノの形をした床のマット、並べ方にあるルールを持っている。

• Bodini, Olivier; Latapy, Matthieu (2003), “Generalized Tilings with Height Functions”, Morfismos 7 (1): 47–68, ISSN 1870-6525, http://www-rp.lip6.fr/%7Elatapy/Publis/morfismos03.pdf .
• Faase, F. (1998). “On the number of specific spanning subgraphs of the graphs G X P_n”. Ars Combin. 49: 129–154. MR1633083. 
• Hock, J. L.; McQuistan, R. B. (1984). “A note on the occupational degeneracy for dimers on a saturated two-dimenisonal lattice space”. Discrete Appl. Math. 8: 101–104. doi:10.1016/0166-218X(84)90083-0. MR0739603. 
• Kasteleyn, P. W. (1961), “The statistics of dimers on a lattice. I. The number of dimer arrangements on a quadratic lattice”, Physica 27 (12): 1209–1225, Bibcode: 1961Phy....27.1209K, doi:10.1016/0031-8914(61)90063-5 .
• Kenyon, Richard (2000), “The planar dimer model with boundary: a survey”, in Baake, Michael; Moody, Robert V., Directions in mathematical quasicrystals, CRM Monograph Series, 13, Providence, RI: American Mathematical Society, pp. 307–328, ISBN 0-8218-2629-8, MR1798998, Zbl 1026.82007 
• Kenyon, Richard; Okounkov, Andrei (2005), “What is … a dimer?”, Notices of the American Mathematical Society 52 (3): 342–343, ISSN 0002-9920, http://www.ams.org/notices/200503/what-is.pdf .
• Klarner, David; Pollack, Jordan (1980), “Domino tilings of rectangles with fixed width”, Discrete Mathematics 32 (1): 45–52, doi:10.1016/0012-365X(80)90098-9, MR588907, Zbl 0444.05009 .
• Mathar, Richard J. (2013). "Paving rectangular regions with rectangular tiles: tatami and non-tatami tilings". arXiv:1311.6135。
• Propp, James (2005), “Lambda-determinants and domino-tilings”, Advances in Applied Mathematics 34 (4): 871–879, arXiv:math.CO/0406301, doi:10.1016/j.aam.2004.06.005 .
• Ruskey, Frank; Woodcock, Jennifer (2009). “Counting fixed-height Tatami tilings”. Electron. J. Combin 16 (1): R126. MR2558263. 
• Sellers, James A. (2002), “Domino tilings and products of Fibonacci and Pell numbers”, Journal of Integer Sequences 5 (Article 02.1.2), http://www.emis.de/journals/JIS/VOL5/Sellers/sellers4.html .
• Stanley, Richard P. (1985). “On dimer coverings of rectangles of fixed width”. Discrete Appl. Math 12: 81–87. doi:10.1016/0166-218x(85)90042-3. MR0798013. 
• Thurston, W. P. (1990), “Conway's tiling groups”, American Mathematical Monthly (Mathematical Association of America) 97 (8): 757–773, doi:10.2307/2324578, JSTOR 2324578, https://jstor.org/stable/2324578 .
• Wells, David (1997), The Penguin Dictionary of Curious and Interesting Numbers (revised ed.), London: Penguin, p. 182, ISBN 0-14-026149-4 .
• 高崎金久『線形代数と数え上げ』日本評論社 (2012) ISBN 978-4535786806