Titik kritis (matematika)

Titik kritis adalah istilah umum yang digunakan dalam banyak cabang matematika.

Ketika berhadapan dengan fungsi dari variabel real, titik kritis adalah titik dalam domain fungsi di mana fungsi tersebut tidak dapat didiferensialkan atau nilai turunannya sama dengan nol.^[1] Ketika berurusan dengan variabel kompleks, titik kritis adalah, sama halnya, titik dalam domain fungsi yang mengakibatkan fungsi tersebut tidak holomorfik atau turunannya sama dengan nol.^[2][3] Demikian juga, untuk fungsi dari beberapa variabel real, titik kritis adalah nilai dalam domainnya sehingga gradiennya tidak terdefinisi atau sama dengan nol.^[4]

Nilai fungsi pada titik kritis disebut dengan nilai kritis.

Definisi semacam ini dapat diperumum ke peta terdiferensialkan antara ${\displaystyle \mathbb {R} ^{m}}$ dan ${\displaystyle \mathbb {R} ^{n}}$. Sebuah titik kritis, dalam hal ini, adalah sebuah titik yang mengakibatkan rank dari matriks Jacobi tidak maksimum. Definisi ini juga dapat diperumum lebih jauh ke peta terdiferensialkan antara lipatan-lipatan terdiferensialkan, sebagai titik-titik yang mengakibatkan rank dari matriks Jacobi berkurang. Dalam hal ini, titik-titik kritis juga disebut titik bifurkasi.

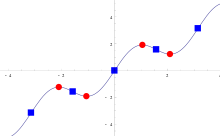
Sebuah titik kritis dari sebuah fungsi variabel satu variabel real, ${\displaystyle f(x)}$, adalah sebuah nilai ${\displaystyle x_{0}}$ dalam domain ${\displaystyle f}$ yang mengakibatkan ${\displaystyle f}$ tidak terdiferensialkan atau turunannya adalah 0 (${\displaystyle f'(x_{0})=0}$).^[1] Nilai kritis adalah nilai fungsi ${\displaystyle f}$ di sebuah titik kritis. Konsep-konsep ini dapat divisualisasikan melalui grafik fungsi ${\displaystyle f}$: pada titik kritis, grafik akan memiliki garis singgung horisontal. Untuk fungsi terdiferensialkan, titik kritis sama dengan titik stasioner.

Meskipun mudah divisualisasikan dengan grafik (yang merupakan sebuah kurva), pengertian titik kritis dari fungsi tidak dapat disamakan dengan pengertian titik kritis dari kurva (lihat bagian di bawah ini untuk definisi yang lebih rinci). Jika ${\displaystyle g(x,\,y)}$ adalah fungsi dua variabel yang terdiferensialkan, maka ${\displaystyle g(x,\,y)=0}$ adalah persamaan implisit dari sebuah kurva. Titik kritis dari kurva seperti itu, untuk proyeksi yang sejajar dengan sumbu-y (pemetaan ${\displaystyle (x,\,y)\to x}$), adalah titik pada kurva yang memenuhi $${\displaystyle {\frac {\partial g}{\partial y}}(x,y)=0.}$$Hal ini mengartikan bahwa garis singgung kurva akan sejajar dengan sumbu-y, dan bahwa pada titik ini, ${\displaystyle g}$ tidak mendefinisikan fungsi implisit dari ${\displaystyle x}$ ke ${\displaystyle y}$ (lihat teorema fungsi implisit). Jika ${\displaystyle (x_{0},\,y_{0})}$ adalah titik kritis, maka ${\displaystyle x_{0}}$ adalah nilai kritisnya. Titik kritis seperti itu juga disebut titik bifurkasi, karena secara umum, ketika nilai ${\displaystyle x}$ berubah disekitar nilai kritis, akan ada dua cabang kurva di sisi ${\displaystyle x_{0}}$ dan nol di sisi lainnya.

Dari definisi-definisi ini dapat disimpulkan bahwa fungsi terdiferensialkan ${\displaystyle f(x)}$ memiliki titik kritis ${\displaystyle x_{0}}$ dengan nilai kritis ${\displaystyle y_{0}}$, jika dan hanya jika ${\displaystyle (x_{0},\,y_{0})}$ adalah titik kritis dari grafik ${\displaystyle f(x)}$ untuk proyeksi yang sejajar dengan sumbu-x. Jika ${\displaystyle f}$ tidak dapat didiferensialkan di ${\displaystyle x_{0}}$ karena garis singgung menjadi sejajar dengan sumbu-y, maka ${\displaystyle x_{0}}$ masih merupakan titik kritis ${\displaystyle f}$, namun dalam kasus ini ${\displaystyle (x_{0},\,y_{0})}$ adalah titik kritis dari grafik fungsi untuk proyeksi yang sejajar dengan sumbu-y. Sebagai contoh, titik kritis dari lingkaran satuan persamaan ${\displaystyle x^{2}+y^{2}-1=0}$ adalah ${\displaystyle (0,\,1)}$ dan ${\displaystyle (0,\,-1)}$ untuk proyeksi sejajar dengan sumbu-x, dan (1, 0) dan (-1, 0) untuk arah sejajar dengan sumbu-y. Jika seseorang menganggap setengah lingkaran atas sebagai grafik fungsi

${\displaystyle f(x)={\sqrt {1-x^{2}}},}$ maka ${\displaystyle x=0}$ adalah titik kritis dengan nilai kritis 1 karena turunannya sama dengan 0, dan ${\displaystyle x=-1}$ dan ${\displaystyle x=1}$ adalah titik kritis dengan nilai kritis 0 karena turunannya tidak terdefinisi.

• Fungsi ${\displaystyle f(x)=x^{2}+2x+3}$ terdiferensialkan dimanapun, dengan turunan ${\displaystyle f'(x)=2x+2}$. Fungsi ini memiliki titik kritis tunggal, yakni -1, yang didapatkan dengan menyelesaikan ${\displaystyle 2x+2=0}$. Titik ini adalah minimum global dari ${\displaystyle f}$.
• Fungsi ${\displaystyle f(x)=x^{\frac {2}{3}}}$ terdefinisi untuk semua ${\displaystyle x}$ dan terdiferensialkan untuk ${\displaystyle x\neq 0}$, dengan turunan ${\displaystyle f'={\tfrac {2}{3}}x^{-{\frac {1}{3}}}.}$ Titik ${\displaystyle x=0}$ adalah titik kritis satu-satunya fungsi ini, karena ${\displaystyle f}$ tidak terdiferensialkan di sana dan karena ${\displaystyle f'(x)\neq 0}$ untuk ${\displaystyle x\neq 0}$. Nilai kritis pada titik tersebut adalah
• Fungsi nilai absolut ${\displaystyle f(x)=|x|}$ terdiferensialkan dimanapun kecuali pada titik kritis ${\displaystyle x=0}$. Pada titik tersebut fungsi memperoleh nilai minimum globalnya, dengan nilai kritis 0.
• Fungsi ${\displaystyle f(x)={\tfrac {1}{x}}}$ tidak memiliki titik kritis. Titik ${\displaystyle x=0}$ bukan titik kritis karena 0 tidak termasuk dalam domain fungsi tersebut.