Équation de continuité

mécanique des fluides

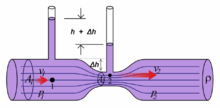
En mécanique des fluides, le principe de conservation de la masse peut être décrit par l'équation de continuité sous plusieurs formes différentes : locale conservative (dérivée en temps normale), locale non conservative (la dérivée en temps suit la particule dans son mouvement), ou intégrale. Suivant les problèmes posés, c'est l'une ou l'autre de ces équations qui pourra être retenue, toutes étant équivalentes. On note ici :

  • ρ = ρ ( x → , t ) {\displaystyle \rho =\rho ({\vec {x}},t)}  : la masse volumique du fluide au point repéré par le vecteur x → {\displaystyle {\vec {x}}} à l'instant t {\displaystyle t}
  • U → = U → ( x → , t ) {\displaystyle {\vec {U}}={\vec {U}}({\vec {x}},t)}  : la vitesse d'une particule de fluide se trouvant au point repéré par le vecteur x → {\displaystyle {\vec {x}}} à l'instant t {\displaystyle t}

Forme locale

Cette écriture est la plus générale et la plus répandue:

∂ ρ ∂ t + ∇ → ⋅ ( ρ   U → ) = 0. {\displaystyle {\frac {\partial \rho }{\partial t}}+{\vec {\nabla }}\cdot \left(\rho \ {\vec {U}}\right)=0.}
En faisant intervenir la notion de dérivée particulaire, on a l'écriture équivalente suivante :
D ρ D t + ρ ∇ → ⋅ ( U → ) = 0. {\displaystyle {\frac {\mathrm {D} \rho }{\mathrm {D} t}}+\rho {\vec {\nabla }}\cdot \left({\vec {U}}\right)=0.}

Forme intégrale

Cette formulation permet l'étude d'un "bloc" de fluide Ω ( t ) {\displaystyle \Omega (t)} pouvant éventuellement se déformer au cours du temps. Elle traduit le fait que la masse du fluide enfermé dans le volume Ω ( t ) {\displaystyle \Omega (t)} est constante, soit

d d t ∫ Ω ( t ) ρ ( x → , t )   d Ω ( t ) = 0. {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\int _{\Omega (t)}\rho \left({\vec {x}},t\right)\ \mathrm {d} \Omega (t)=0.}

Écoulement incompressible

Dans le cas où la masse volumique est constante au cours du temps et uniforme dans l'espace (écoulement incompressible), l'équation de conservation se réduit à ∇ → ⋅ ( U → ) = 0 {\textstyle {\vec {\nabla }}\cdot \left({\vec {U}}\right)=0} .

Conditions de saut

Lorsque le composé étudié est constitué de deux parties du fluide différentes (soit dans Ω 1 {\displaystyle \Omega _{1}} et Ω 2 {\displaystyle \Omega _{2}} ), séparées par une interface Γ ( t ) {\displaystyle \Gamma (t)} se déplaçant à une vitesse de propagation locale W → ( x → , t ) {\displaystyle {\vec {W}}\left({\vec {x}},t\right)} , la conservation de la masse s'exprime par la relation suivante :

[ ρ ( U → − W → ) ⋅ n → ] = 0 , {\displaystyle \left[\rho \left({\vec {U}}-{\vec {W}}\right)\cdot {\vec {n}}\right]=0,}
où [ f ] = f ∣ Ω 2 ∩ Γ ( t ) − f ∣ Ω 1 ∩ Γ ( t ) {\displaystyle [f]=f\mid _{\Omega _{2}\cap \Gamma (t)}-f\mid _{\Omega _{1}\cap \Gamma (t)}} où f ∣ Ω i ∩ Γ ( t ) {\displaystyle f\mid _{\Omega _{i}\cap \Gamma (t)}} est la valeur du fluide dans Ω i {\displaystyle \Omega _{i}} proche de l'interface Γ ( t ) {\displaystyle \Gamma (t)} et n → {\displaystyle {\vec {n}}} est le vecteur normal extérieur à Ω 1 ∩ Γ ( t ) {\displaystyle \Omega _{1}\cap \Gamma (t)} . Ceci est à la base des relations de Rankine-Hugoniot.

Articles connexes

Sur les autres projets Wikimedia :

  • Conservation de la masse et équation de continuité, sur Wikiversity
v · m
Branches
  • Statique des fluides
  • Dynamique des fluides
  • Hydraulique
Fluides
Écoulements
Comportement rhéologique
Équations
Nombres sans dimension
  • icône décorative Portail de la physique